Special automorphism

constructed from an automorphism 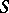of a measure space 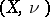and a function 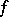(defined on 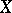and taking positive integral values)

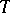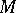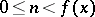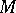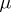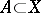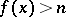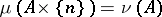An automorphism of a certain new measure space constructed in the following way. The points of are the pairs where and is an integer, , and is equipped with the obvious measure : if and for all , then . If 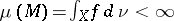, then one usually normalizes this measure. Let 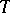be the transformation that increases the second coordinate of the point 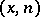by one if 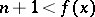(i.e. if the transformed point remains within 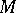), and otherwise put 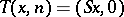. The transformation 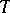turns out to be an automorphism of the measure space .

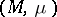The above construction is often applied in ergodic theory when constructing various examples. On the other hand, the role of special automorphisms is clear from the following. By identifying each point 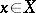with 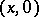, one may assume that 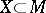. Then 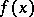is the time spent by a point that starts in 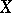and moves under the action of the cascade 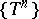to return once again to 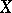, and 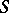is the induced automorphism 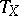. Thus, special automorphisms can be used to recover the trajectories of a dynamical system in the whole phase space by observing only the passages of the moving point through the set .

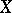Comments

Instead of "special automorphism constructed from an automorphism S" one also speaks of a primitive of 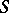. (In that case what was called above the "induced automorphism" is called a derivative of 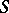. See [a2].) The idea goes back to S. Kakutani; cf. [a1].

References

[a1]	S. Kakutani, "Induced measure preserving transformations" Proc. Japan Acad. , 19 (1943) pp. 635–641
[a2]	K. Petersen, "Ergodic theory" , Cambridge Univ. Press (1983) pp. 39
[a3]	I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) pp. Chapt. 1, §5 (Translated from Russian)