Ceva theorem
A theorem on the relation between the lengths of certain lines intersecting a triangle. Let  be three points lying, respectively, on the sides
be three points lying, respectively, on the sides  ,
,  and
and  of a triangle
of a triangle  . For the lines
. For the lines  ,
,  and
and  to intersect in a single point or to be all parallel it is necessary and sufficient that
to intersect in a single point or to be all parallel it is necessary and sufficient that
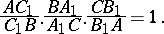 |
Lines  ,
, 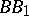 and
and 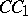 that meet in a single point and pass through the vertices of a triangle are called Ceva, or Cevian, lines. Ceva's theorem is metrically dual to the Menelaus theorem. It is named after G. Ceva [1].
that meet in a single point and pass through the vertices of a triangle are called Ceva, or Cevian, lines. Ceva's theorem is metrically dual to the Menelaus theorem. It is named after G. Ceva [1].
Ceva's theorem can be generalized to the case of a polygon. Let a point  be given in a planar polygon with an odd number of vertices
be given in a planar polygon with an odd number of vertices  , and suppose that the lines
, and suppose that the lines 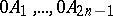 intersect the sides of the polygon opposite to
intersect the sides of the polygon opposite to 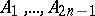 respectively in points
respectively in points 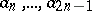 ,
,  . In this case
. In this case
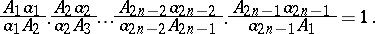 |
References
| [1] | G. Ceva, "De lineis rectis se invicem secantibus statica constructio" , Milano (1678) |
Comments
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) |
Ceva theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ceva_theorem&oldid=33015