Schreier system

A non-empty subset of a free group 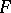with set of generators 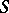, satisfying the following condition. Let an element 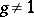of the Schreier system be represented as a reduced word in the generators of the group:

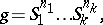and let

It is required then, that the element 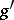should also belong to this system (the element 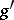can be considered as the reduced word obtained from 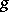by deleting its last letter). The element 1 belongs to every Schreier system.

Introduced by O. Schreier in the 1920s, see [1].

References

[1]	W.S. Massey, "Algebraic topology: an introduction" , Springer (1977)

Comments

Of particular interest are Schreier systems which are systems of representations of the cosets of a subgroup. Cf. [a1] for some uses of Schreier systems, such as a proof of the Nielsen–Schreier theorem that subgroups of free groups are free.

References

[a1]	W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) pp. 93