Asymptotic sequence

A sequence of functions 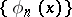such that

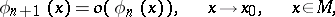where 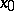is a limit point of the set (finite or infinite). If the nature of 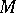is clear from the context, then one simply writes 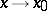. If 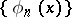is an asymptotic sequence and 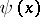is a function defined on 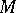, then 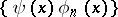will also be an asymptotic sequence.

Examples of asymptotic sequences:

1) ;

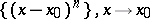2) ;

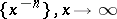3) ;

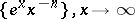4) 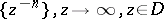, where 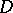is an unbounded domain in the complex plane. Asymptotic sequences such as 1), 2) and 4) are called asymptotic power sequences.

References

[a1]	N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981)
[a2]	A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956)