Laplace integral
From Encyclopedia of Mathematics
An integral of the form
 |
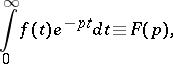that defines the integral Laplace transform of a function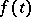 
of a real variable 
, 
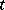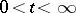, giving a function 
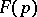of a complex variable 
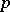. It was considered by P. Laplace at the end of the eighteenth and beginning of the 19th century; it was used by L. Euler in 1737.
Two specific definite integrals depending on the parameters 
:
 |
 |
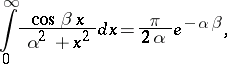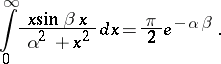Comments
References
| [a1] | F. Oberhettinger, L. Badii, "Tables of Laplace transforms" , Springer (1973) |
| [a2] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) pp. Chapt. 6 |
| [a3] | V.A. Ditkin, A.P. Prudnikov, "Integral transforms" , Plenum (1969) (Translated from Russian) |
| [a4] | G. Doetsch, "Handbuch der Laplace-Transformation" , 1–3 , Birkhäuser (1950–1956) |
How to Cite This Entry:
Laplace integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace_integral&oldid=32990
Laplace integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace_integral&oldid=32990
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article