Carter subgroup

A maximal nilpotent subgroup of a group that coincides with its normalizer. Introduced by R. Carter [1]. Any finite solvable group 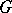has a Carter subgroup, and all Carter subgroups of 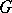are conjugate (Carter's theorem).

References

[1]	R.W. Carter, "Nilpotent selfnormalizing subgroups of soluble groups" Math. Z. , 75 : 2 (1961) pp. 136–139
[2]	A.I. Kostrikin, "Finite groups" Itogi Nauk. Algebra 1964 (1966) pp. 7–46 (In Russian)

Comments

An example of a non-solvable group having no Carter subgroup is 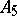, the alternating group of order 5.

Any Carter subgroup of a finite solvable group is a maximal nilpotent subgroup.

References

[a1]	B. Huppert, "Endliche Gruppen" , 1 , Springer (1979) pp. 482–490