Semi-elliptic space

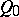A projective -space in which the metric is defined by a given absolute, which is the aggregate of an imaginary quadratic cone with an 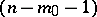-flat vertex 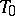, an 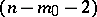-imaginary cone 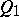with an 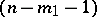-flat vertex 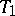in the 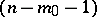-plane 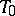, etc., up to an 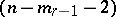-imaginary cone 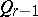with an 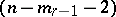-flat vertex 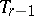and a non-degenerate imaginary 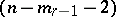-quadratic 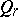in the 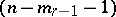-plane 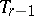, 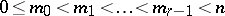. The indices of the cones 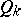, , 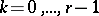are: 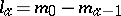, 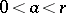; 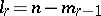. A semi-elliptic space is denoted by .

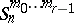In case the cone 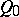is a pair of merging planes coinciding with the plane 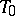(for 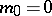), the space with the improper plane 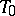is called the semi-Euclidean space .

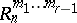The distance between two points 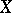and 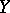is defined according to the position of the straight line 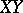with respect to the planes 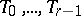. If, in particular, the line 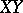does not intersect the plane 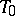, then the distance between the points 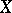and 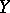is defined in terms of the scalar product, analogously to the distance in a quasi-elliptic space. If, however, the line 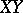intersects the plane 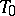but does not intersect the plane 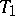, or intersects the plane 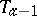but does not intersect the plane 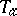, the distance between the points is defined using the scalar square of the difference of the corresponding vectors of the points 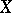and .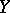

According to the position with respect to the planes of the absolute in a semi-elliptic space, one distinguishes four types of straight lines.

The angles between planes in a semi-elliptic space are defined analogously to angles between planes in a quasi-elliptic space, that is, by using distances in the dual space.

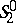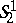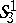A projective metric in a semi-elliptic space is a metric of a very general type. A particular case of the metric in a semi-elliptic space is, for example, the metric of a quasi-elliptic space. In particular, the -plane coincides with the Euclidean and with the co-Euclidean plane; the -space with the quasi-elliptic and 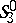with the Euclidean -space; the -space 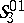is Galilean, 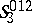is a flag space, etc. The -space 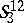corresponds by the duality principle to the Galilean -space 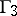and is called the co-Galilean space. (The absolute of a co-Galilean space consists of a pair of imaginary planes (the cone 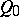) and a point 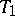on the straight line 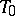of intersection of these planes.)

The motions of a semi-elliptic space are the collineations of it taking the absolute into itself. In the case 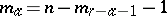, , 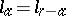the semi-elliptic space is dual to itself, and has co-motions defined in it analogously to co-motions in a quasi-elliptic space.

The motions, and the motions and co-motions form Lie groups. The motions (as well as the co-motions) are described by orthogonal operators.

A semi-elliptic space is a semi-Riemannian space.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)