Ample sheaf
A generalization of the concept of an ample invertible sheaf. Let 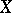 be a Noetherian scheme over a field
be a Noetherian scheme over a field 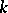 , and let
, and let 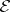 be a locally free sheaf on
be a locally free sheaf on 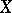 (that is, the sheaf of sections of some algebraic vector bundle
(that is, the sheaf of sections of some algebraic vector bundle 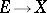 ). The sheaf
). The sheaf 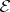 is called ample if for each coherent sheaf
is called ample if for each coherent sheaf 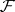 on
on 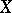 there exists an integer
there exists an integer 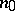 , depending on
, depending on 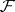 , such that the sheaf
, such that the sheaf 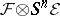 for
for 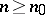 is generated by its global sections (here
is generated by its global sections (here 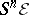 denotes the
denotes the  -th symmetric power of
-th symmetric power of  ).
).
A locally free sheaf 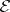 on
on 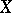 is ample if and only if the invertible tautological sheaf
is ample if and only if the invertible tautological sheaf 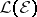 on the projectivization
on the projectivization 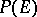 of the bundle
of the bundle 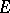 is ample. Another criterion of ampleness is that for each coherent sheaf
is ample. Another criterion of ampleness is that for each coherent sheaf 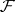 on
on 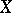 there must exist an integer
there must exist an integer 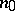 , depending on
, depending on 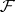 , such that the cohomology group
, such that the cohomology group 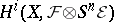 is zero for
is zero for 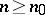 and
and 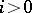 . If the sheaves
. If the sheaves 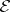 and
and 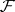 are ample then
are ample then 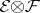 is an ample sheaf [1]. If
is an ample sheaf [1]. If 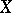 is a non-singular projective curve, then a sheaf
is a non-singular projective curve, then a sheaf 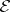 on
on 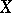 is ample if and only if
is ample if and only if 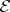 and all its quotient sheaves have positive degree [2]. The tangent sheaf on
and all its quotient sheaves have positive degree [2]. The tangent sheaf on 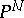 is ample for any
is ample for any 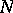 (see [1]). The converse also holds: Any non-singular
(see [1]). The converse also holds: Any non-singular 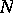 -dimensional algebraic variety with an ample tangent sheaf is isomorphic to
-dimensional algebraic variety with an ample tangent sheaf is isomorphic to 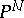 (see [1], [3]).
(see [1], [3]).
References
| [1] | R. Hartshorne, "Ample vector bundles" Publ. Math. IHES , 29 (1966) pp. 319–350 |
| [2] | R. Hartshorne, "Ample vector bundles on curves" Nagoya Math. J. , 43 (1971) pp. 73–89 |
| [3] | M. Demazure, "Charactérisations de l'espace projectif (conjectures de Hartshorne et de Frankel)" , Sem. Bourbaki 1979/80 , Lect. notes in math. , 842 , Springer (1981) pp. 11–19 |
Comments
The theorem stated in the last line of the text is due to S. Mori [a1].
References
| [a1] | S. Mori, "Positive manifolds with ample tangent bundles" Ann. of Math. , 110 (1979) pp. 593–606 |
Ample sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ample_sheaf&oldid=32973