Analytic functional
From Encyclopedia of Mathematics
An element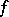 
of the space 
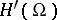, the dual of the space 
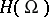of analytic functions defined on an open subset 
of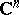 
, i.e. a functional on 
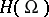. Thus, a distribution with compact support is an analytic functional. There exists a compact set 
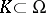, said to be the support of the analytic functional 
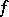, on which 
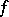is concentrated: For any open set 
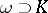the functional 
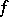can be extended to 
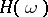so that for all 
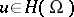the following inequality is valid:
 |
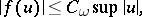where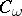 
is a constant depending on 
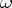. There exists a measure 
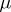with support in 
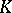such that
 |
An analytic functional is defined in a similar manner on a space of real-valued functions.
Comments
For applications to partial differential equations, see [a1].
References
| [a1] | L. Ehrenpreis, "Fourier analysis in several complex variables" , Wiley (Interscience) (1970) |
| [a2] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Sect. 4.5 |
How to Cite This Entry:
Analytic functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_functional&oldid=32972
Analytic functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_functional&oldid=32972
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article