Men'shov-Rademacher theorem
From Encyclopedia of Mathematics
Revision as of 18:53, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Men'shov–Rademacher theorem to Men'shov-Rademacher theorem: ascii title)
A theorem on the almost-everywhere convergence of orthogonal series: If a system of functions  is orthonormal on a segment
is orthonormal on a segment 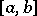 and if
and if
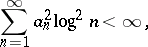 |
then the series
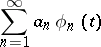 | (*) |
converges almost-everywhere on 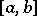 . This result has been proved independently by D.E. Men'shov [1] and H. Rademacher [2]. Men'shov showed also that this assertion is sharp in the following sense. If a monotone increasing sequence
. This result has been proved independently by D.E. Men'shov [1] and H. Rademacher [2]. Men'shov showed also that this assertion is sharp in the following sense. If a monotone increasing sequence  satisfies the condition
satisfies the condition 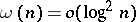 , then one can find an orthogonal series (*), diverging everywhere, the coefficients of which satisfy the condition
, then one can find an orthogonal series (*), diverging everywhere, the coefficients of which satisfy the condition
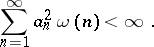 |
References
| [1] | D.E. Men'shov, "Sur la séries de fonctions orthogonales (I)" Fund. Math. , 4 (1923) pp. 82–105 |
| [2] | H. Rademacher, "Einige Sätze über Reihen von allgemeinen Orthogonalfunktionen" Math. Ann. , 87 (1922) pp. 112–138 |
| [3] | G. Alexits, "Konvergenzprobleme der Orthogonalreihen" , Deutsch. Verlag Wissenschaft. (1960) |
Comments
References
| [a1] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Men'shov-Rademacher theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Men%27shov-Rademacher_theorem&oldid=32971
Men'shov-Rademacher theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Men%27shov-Rademacher_theorem&oldid=32971
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article