Recurrence relation
recurrence formula
A relation of the form
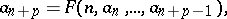 |
permitting one to compute all members of the sequence  if its first
if its first  members are given. Examples of recurrence relations are: 1)
members are given. Examples of recurrence relations are: 1) 
 , a geometric progression; 2)
, a geometric progression; 2)  , an arithmetic progression; 3)
, an arithmetic progression; 3)  , the sequence of Fibonacci numbers.
, the sequence of Fibonacci numbers.
In the case where the recurrence relation is linear (see Recursive sequence) the problem of describing the set of all sequences that satisfy a given recurrence relation has an analogy with solving an ordinary homogeneous linear differential equation with constant coefficients.
References
| [1] | A.I. Markushevich, "Rekursive Folgen" , Deutsch. Verlag Wissenschaft. (1973) (Translated from Russian) |
Comments
A sequence of elements  of a commutative ring
of a commutative ring  with a unit element satisfies a linear recurrence relation
with a unit element satisfies a linear recurrence relation 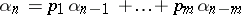 ,
, 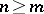 , if and only if the formal power series
, if and only if the formal power series 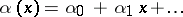 is a rational function of the form
is a rational function of the form 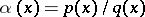 , with
, with 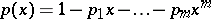 and
and 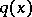 a polynomial of degree
a polynomial of degree 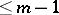 .
.
Recurrence relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recurrence_relation&oldid=32959