Vortical ring

A vortical thread having the shape of a torus of small cross-section. The general formulas which determine the velocity of liquid particles from vortices make it possible to represent the velocity potential 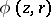and the Stokes function of the current 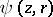of a flow generated in an unbounded liquid by a vortical ring as integrals containing the Bessel functions of order zero and one:

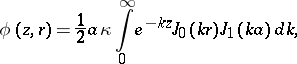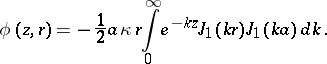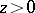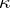In these formulas, which apply if , is the radius of the ring and is the stress of the vortical ring. The coordinate is taken from the plane of the moving ring. The ring, when acted upon by the velocities it itself produces in the ring, moves in the direction of the -axis at a constant velocity , which is given by the following approximate formula:

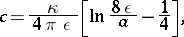where is the radius of a cross-section of the vortical ring. For several vortical rings the functions 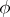and 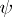are represented as sums of the respective functions of each ring.

References

[1]	L.M. Milne-Thomson, "Theoretical hydrodynamics" , Macmillan (1950)