Quadratic reciprocity law

The relation

connecting the Legendre symbols (cf. Legendre symbol)

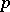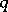for different odd prime numbers and . There are two additions to this quadratic reciprocity law, namely:

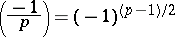and

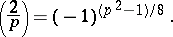C.F. Gauss gave the first complete proof of the quadratic reciprocity law, which for this reason is also called the Gauss reciprocity law.

It immediately follows from this law that for a given square-free number 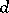, the primes 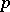for which 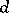is a quadratic residue modulo 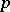ly in certain arithmetic progressions with common difference 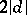or 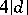. The number of these progressions is 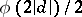or 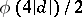, where 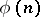is the Euler function. The quadratic reciprocity law makes it possible to establish factorization laws in quadratic extensions 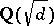of the field of rational numbers, since the factorization into prime factors in 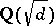of a prime number that does not divide 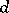depends on whether or not 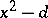is reducible modulo .

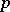References

[1]	I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)
[2]	Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)

Comments

See also Quadratic residue; Dirichlet character.

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII