Dedekind eta-function
From Encyclopedia of Mathematics
The function defined by
 |
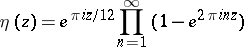for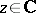 
, 
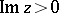. As the infinite product converges absolutely, uniformly for 
in compact sets (cf. Uniform convergence), the function 
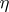is holomorphic (cf. Analytic function). Moreover, it satisfies 
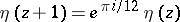and 
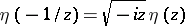. So,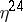 
is a modular form of weight 
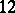(cf. also Modular group).
R. Dedekind [a1] comments on computations of B. Riemann in connection with theta-functions (cf. Theta-function). He shows that it is basic to understand the transformation behaviour of the logarithm of the function now carrying his name. This study leads him to quantities now called Dedekind sums (cf. Dedekind sum). See [a2], Chapt. IV, for a further discussion.
References
| [a1] | R. Dedekind, "Erläuterungen zu den fragmenten XXVIII" H. Weber (ed.) , B. Riemann: Gesammelte mathematische Werke und wissenschaftlicher Nachlass , Dover, reprint (1953) |
| [a2] | H. Rademacher, E. Grosswald, "Dedekind sums" , Math. Assoc. America (1972) |
How to Cite This Entry:
Dedekind eta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_eta-function&oldid=32932
Dedekind eta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_eta-function&oldid=32932
This article was adapted from an original article by R.W. Bruggeman (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article