Denjoy-Luzin theorem
on absolutely convergent trigonometric series
If the trigonometric series
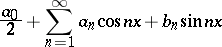 | (1) |
converges absolutely on a set of positive Lebesgue measure, then the series made up of the absolute values of its coefficients,
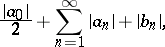 | (2) |
converges and, consequently, the initial series (1) converges absolutely and uniformly on the entire real axis. However, the property of the absolute convergence set of the series (1) being of positive measure, which according to A. Denjoy and N.N. Luzin is sufficient for the series (2) to converge, is not necessary. There exist, for example, perfect sets of measure zero, the absolute convergence on which of the series (1) entails the convergence of the series (2).
The theorem was independently established by Denjoy [1] and by Luzin [2]; various generalizations of it also exist [3].
References
| [1] | A. Denjoy, "Sur l'absolue convergence des séries trigonométriques" C.R. Acad. Sci. , 155 (1912) pp. 135–136 |
| [2] | N.N. Luzin, Mat. Sb. , 28 (1912) pp. 461–472 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Comments
For generalizations see, e.g., [a1], Chapt. 6.
References
| [a1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
Denjoy-Luzin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Denjoy-Luzin_theorem&oldid=32928