Maximin criterion

maximin test

A statistical test for testing a compound hypothesis 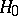: 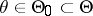against the compound alternative 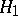: 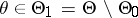, whose minimal power (cf. Power of a statistical test) is maximal in the class of all statistical tests intended for testing 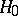against 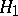and having the same size 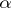, 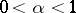. In statistically testing 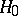against 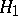a maximin invariant test exists if the problem itself is invariant relative to some group of transformations 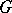, and there is a uniformly most-powerful test in the class of corresponding invariant tests (cf. Hunt–Stein theorem). 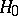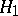A maximin test exists, in general, if the family of probability distributions determined by the null and competing hypotheses and is absolutely continuous relative to some 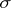-finite measure.

References

[1]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959)
[2]	J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)