Matching polynomial of a graph

A matching cover (or simply a matching) in a graph 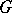is taken to be a subgraph of 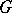consisting of disjoint (independent) edges of 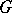, together with the remaining nodes of 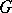as (isolated) components. A matching is called a 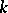-matching if it contains exactly 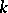edges. If 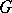contains 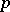nodes, then the extreme cases are:

i) 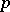is even and 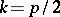; in this case, all the nodes of 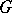are covered with edges (a perfect matching); and

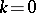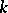ii) ; in this case, none of the nodes of are covered by edges (the empty graph). If a matching contains edges, then it will have 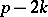component nodes. Now assign weights (or indeterminates over the complex numbers) 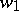and 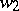to each node and edge of 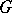, respectively. Take the weight of a matching to be the product of the weights of all its components. Then the weight of a 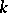-matching will be 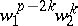. The matching polynomial of 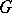, denoted by 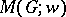, is the sum of the weights of all the matchings in 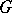. Setting 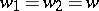, then the resulting polynomial is called the simple matching polynomial of .

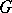The matching polynomial was introduced in [a1]. Basic algorithms for finding matching polynomials of arbitrary graphs, basic properties of the polynomial, and explicit formulas for the matching polynomials of many well-known families of graphs are given in [a1]. The coefficients of the polynomial have been investigated [a8]. The analytical properties of the polynomial have also been investigated [a10].

Various polynomials used in statistical physics and in chemical thermodynamics can be shown to be matching polynomials. The matching polynomial is related to many of the well-known classical polynomials encountered in combinatorics. These include the Chebyshev polynomials, the Hermite polynomials and the Laguerre polynomials. An account of these and other connections can be found in [a14], [a16]. The classical rook polynomial is also a special matching polynomial; and in fact, rook theory can be developed entirely through matching polynomials (see [a4], [a5]). The matching polynomial is also related to various other polynomials encountered in graph theory. These include the chromatic polynomial (see [a13]), the characteristic polynomial and the acyclic polynomial (see [a15] and [a3]). The matching polynomial itself is one of a general class of graph polynomials, called F-polynomials (see [a2]). Two graphs are called co-matching if and only if they have the same matching polynomial. A graph is called matching unique if and only if no other graph has the same matching polynomial. Co-matching graphs and matching unique graphs have been investigated (see [a6], [a9]). It has been shown that the matching polynomial of certain graphs (called D-graphs) can be written as determinants of matrices. It appears that for every graph there exists a co-matching D-graph. The construction of co-matching D-graphs is one the main subjects of current interest in the area (see [a7], [a11], [a12]).

References

[a1]	E.J. Farrell, "Introduction to matching polynomials" J. Combin. Th. B , 27 (1979) pp. 75–86
[a2]	E.J. Farrell, "On a general class of graph polynomials" J. Combin. Th. B , 26 (1979) pp. 111–122
[a3]	E.J. Farrell, "The matching polynomial and its relation to the acyclic polynomial of a graph" Ars Combinatoria , 9 (1980) pp. 221–228
[a4]	E.J. Farrell, "The matching polynomial and its relation to the Rook polynomial" J. Franklin Inst. , 325 : 4 (1988) pp. 527–536
[a5]	E.J. Farrell, "A graph-theoretic approach to Rook theory" Caribb. J. Math. , 7 (1988) pp. 1–47
[a6]	E.J. Farrell, J.M. Guo, "On the characterizing properties of the matching polynomial" Vishwa Internat. J. Graph Th. , 2 : 1 (1993) pp. 55–62
[a7]	E.J. Farrell, S.A. Wahid, "Matching polynomials: A matrix approach and its applications" J. Franklin Inst. , 322 (1986) pp. 13–21
[a8]	E.J. Farrell, J.M. Guo, G.M. Constantine, "On the matching coefficients" Discr. Math. , 89 (1991) pp. 203–210
[a9]	E.J. Farrell, S.A. Wahid, "Some general classes of comatching graphs" Internat. J. Math. Math. Sci. , I0 : 3 (1987) pp. 519–524
[a10]	E.J. Farrell, S.A. Wahid, "Some analytical properties of the matching polynomial of a graph" , Proc. Fifth Caribb. Conf. in Comb. and Graph Th., Jan.5-8, 1988 pp. 105–119
[a11]	E.J. Farrell, S.A. Wahid, "D-graphs I: An introduction to graphs whose matching polynomials are determinants of matrices" Bull. ICA , 15 (1995) pp. 81–86
[a12]	E.J. Farrell, S.A. Wahid, "D-graphs II: Constructions of D-graphs for some families of graphs with even cycles" Utilitas Math. , 56 (1999) pp. 167–176
[a13]	E.J. Farrell, E.G. Whitehead, "Connections between the matching and chromatic polynomials" Internat. J. Math. Math. Sci. , 15 : 4 (1992) pp. 757–766
[a14]	I. Gutman, "The matching polynomial" MATCH : 6 (1979) pp. 75–91
[a15]	I. Gutman, "The acyclic polynomial of a graph" Publ. Inst. Math. Beograd , 22 (36) (1977) pp. 63–69
[a16]	C.D. Godsil, I. Gutman, "On the theory of the matching polynomial" J. Graph Th. , 5 (1981) pp. 137–145