Pythagorean theorem, multi-dimensional
From Encyclopedia of Mathematics
Consider the  -dimensional space
-dimensional space 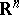 (with the usual metric and measure). Let
(with the usual metric and measure). Let 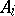 be a point on the
be a point on the 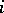 th coordinate axis and let
th coordinate axis and let  be the origin. Let
be the origin. Let  be the
be the 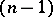 -dimensional volume of the
-dimensional volume of the  -dimensional simplex
-dimensional simplex  and let
and let  be the
be the  -dimensional volume of the
-dimensional volume of the  -dimensional simplex
-dimensional simplex 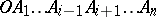 . Then
. Then  .
.
For other and further generalizations of the classical Pythagoras theorem, see [a2] and the references therein.
References
| [a1] | Etsua Yoshinaga, Shigeo Akiba, "Very simple proofs of the generalized Pythagorean theorem" Sci. Reports Yokohama National Univ. Sect. I , 42 (1995) pp. 45–46 |
| [a2] | D.R. Conant, W.A. Beyer, "Generalized Pythagorean theorem" Amer. Math. Monthly , 81 (1974) pp. 262–265 |
How to Cite This Entry:
Pythagorean theorem, multi-dimensional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pythagorean_theorem,_multi-dimensional&oldid=32914
Pythagorean theorem, multi-dimensional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pythagorean_theorem,_multi-dimensional&oldid=32914
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article