Icosahedral space
From Encyclopedia of Mathematics
The three-dimensional space that is the orbit space of the action of the binary icosahedron group on the three-dimensional sphere. It was discovered by H. Poincaré as an example of a homology sphere of genus 2 in the consideration of Heegaard diagrams (cf. Heegaard diagram). The icosahedral space is a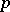 
-sheeted covering of 
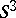ramified along a torus knot of type 
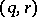, where 
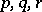is any permutation of the numbers 
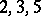. The icosahedral space can be defined analytically as the intersection of the surface
 |
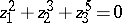in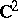 
with the unit sphere. Finally, the icosahedral space can be identified with the dodecahedral space.
Comments
References
| [a1] | H. Seifert, W. Threlfall, "Lehrbuch der Topologie" , Chelsea, reprint (1947) |
How to Cite This Entry:
Icosahedral space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Icosahedral_space&oldid=32908
Icosahedral space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Icosahedral_space&oldid=32908
This article was adapted from an original article by A.V. Chernavskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article