Signal extraction

in a noise background

A branch of statistical communication theory. The mathematical problems of signal extraction are statistical problems of the theory of stochastic processes (see also Information theory). A number of typical problems in signal extraction are listed below.

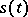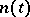A message , which may be a random or a non-random function of a certain structure, is converted into a signal , where is a stochastic process (a noise), while 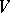(the communication channel) is an operator which converts the pair into the received signal . It is usually assumed that the effect of the noise on the signal is additive: 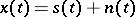. In such a situation the problems of signal extraction are as outlined below.

1) Detection of the signal, that is, checking the hypothesis 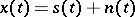(a signal is present) against the alternative 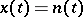(a signal is absent). More involved varieties of the initial hypothesis are also studied: 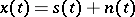starting from some moment, possibly random, of time , which is the moment of appearance of the signal. Here arises the problem of estimating .

2) Differentiating between signals, that is, checking the hypothesis 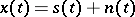, , 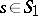against the hypothesis 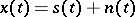, , 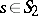where 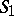and are two different sets of signals.

3) Filtering (reconstruction of a signal), that is, finding statistical estimates for the values of the signal 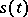at a point , after 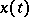, , 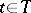has been received.

See also Statistical hypothesis; Stochastic processes, filtering of.

References

[1]	W.B. Davenport, W.L. Root, "An introduction to the theory of random signals and noise" , McGraw-Hill (1970)
[2]	A.A. Kharkevich, "Channels with noise" , Moscow (1965) (In Russian)

References

[a1]	J.M. Wozencraft, I.M. Jacobs, "Principles of communication engineering" , Wiley (1965)
[a2]	C.W. Helstrom, "Statistical theory of signal detection" , Pergamon (1968)