Bourget function
From Encyclopedia of Mathematics
The function 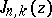 which may be defined as a generalization of the integral representation of the Bessel functions
which may be defined as a generalization of the integral representation of the Bessel functions
 |
where  is an integer and
is an integer and 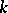 is a positive integer. The integration contour makes one counter-clockwise turn around the coordinate origin. In other words,
is a positive integer. The integration contour makes one counter-clockwise turn around the coordinate origin. In other words,
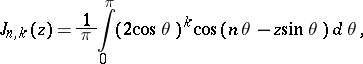 |
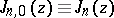 is a cylinder function of the first kind. So named after J. Bourget [1], who studied the function with a view to various applications in astronomy.
is a cylinder function of the first kind. So named after J. Bourget [1], who studied the function with a view to various applications in astronomy.
References
| [1] | J. Bourget, "Mémoire sur les nombres de Cauchy et leur application à divers problèmes de mécanique céleste" J. Math. Pures Appl. (2) , 6 (1861) pp. 32–54 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952) pp. Chapt. 10 |
How to Cite This Entry:
Bourget function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bourget_function&oldid=32896
Bourget function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bourget_function&oldid=32896
This article was adapted from an original article by V.I. Pagurova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article