Rate of convergence

A characteristic of an iterative method that enables one to make a judgement on the dependence of the error of the method at the -th iteration on the number (see [1]–[3]). For example, if 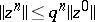, where 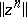is the norm of the error at the -th iteration, while 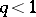, then one says that the method converges with the rate of a geometric progression with denominator 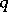, while the value 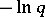is called the asymptotic rate of convergence.

Given inequalities of the type 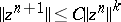, one speaks of a polynomial rate of convergence of order 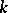(for example, the quadratic rate of convergence of the Newton–Kantorovich iteration method, cf. Kantorovich process).

References

[1]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)
[2]	G.I. Marchuk, "Methods of numerical mathematics" , Springer (1982) (Translated from Russian)
[3]	A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian)
[4]	L.A. Hageman, D.M. Young, "Applied iterative methods" , Acad. Press (1981)
[5]	J.F. Traub, "Iterative methods for the solution of equations" , Prentice-Hall (1964)

Comments

Of course, one can speak of the rate of convergence of any process (not just iterative) in which convergence plays a role. See, in particular, Approximation of functions (and related articles).