Uniformly most-powerful test

A statistical test of given significance level for testing a compound hypothesis 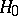against a compound alternative 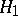, whose power is not less than the power of any other statistical test for testing 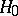against 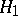of the same significance level (cf. Power of a statistical test).

Suppose that a compound hypothesis 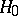: 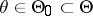has to be tested against the compound alternative 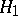: 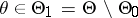, and there is given an upper bound 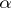, , 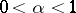for the probability of an error of the first kind, made by rejecting 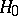when it is in fact true (the number 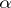is called the significance level of the test, and it is said that the test has level 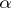). In this way, the restriction on the probability of an error of the first kind reduces the set of tests for testing 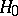against 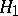to the class of tests of level 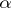. In terms of the power function (cf. Power function of a test) 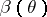, , 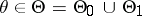a statistical test of fixed significance level 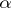means that

If, in the class of all tests of level 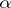for testing 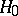against 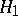, there is one whose power function satisfies

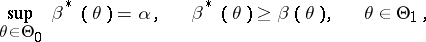where 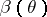is the power function of any other test from this class, then this test is called a uniformly most-powerful test of level 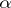for testing 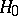against 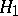. A uniformly most-powerful test is optimal if the comparison is made in terms of the power of tests.

References

[1]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959)