Fourier indices of an almost-periodic function
From Encyclopedia of Mathematics
The real numbers 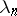 in the Fourier series corresponding to the given almost-periodic function
in the Fourier series corresponding to the given almost-periodic function 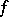 :
:
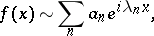 |
where the  are the Fourier coefficients of
are the Fourier coefficients of  (cf. Fourier coefficients of an almost-periodic function; Fourier series of an almost-periodic function). The set of Fourier indices of a function
(cf. Fourier coefficients of an almost-periodic function; Fourier series of an almost-periodic function). The set of Fourier indices of a function 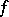 is called its spectrum. In contrast to the periodic case, the spectrum of an almost-periodic function can have finite limit points and can even be everywhere dense. Therefore, the behaviour of the Fourier series of an almost-periodic function depends in an essential way on the arithmetic structure of its spectrum.
is called its spectrum. In contrast to the periodic case, the spectrum of an almost-periodic function can have finite limit points and can even be everywhere dense. Therefore, the behaviour of the Fourier series of an almost-periodic function depends in an essential way on the arithmetic structure of its spectrum.
How to Cite This Entry:
Fourier indices of an almost-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_indices_of_an_almost-periodic_function&oldid=32872
Fourier indices of an almost-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_indices_of_an_almost-periodic_function&oldid=32872
This article was adapted from an original article by E.A. Bredikhina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article