Exceptional value
A concept in value-distribution theory. Let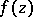 
be a meromorphic function in the whole 
-plane and let 
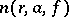denote its number of 
-points (counting multiplicities) in the disc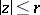 
. According to R. Nevanlinna's first fundamental theorem (cf. [1]), as 
,
 |
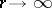where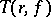 
is the characteristic function, which does not depend on 
, 
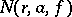is the counting function (the logarithmic average of 
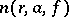) and 
is a function expressing the average proximity of the values of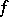 
to 
on 
(cf. Value-distribution theory). For the majority of values 
the quantities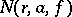 
and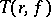 
are asymptotically equivalent, as 
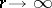. A (finite or infinite) number 
is called an exceptional value if this equivalence as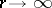 
is violated. One distinguishes several kinds of exceptional values.
A number 
is called an exceptional value of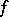 
in the sense of Poincaré if the number of 
-points of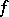 
in the whole plane is finite (cf. [1], [2]), in particular if 
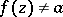for any 
.
A number 
is called an exceptional value of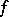 
in the sense of Borel if 
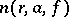grows slower, in a certain sense, than 
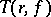, as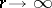 
(cf. [1], [2]).
A number 
is called an exceptional value of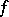 
in the sense of Nevanlinna (cf. [1]) if its defect (cf. Defective value)
 |
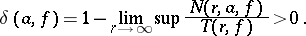A number 
is called an exceptional value of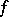 
in the sense of Valiron if
 |
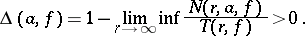A number 
for which
 |
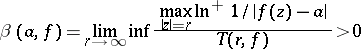is also called an exceptional value for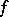 
. The quantity 
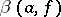(the positive deviation of 
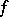) characterizes the rate of the asymptotic approximation of 
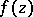to 
(cf. [3]).
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | A.A. Gol'dberg, I.V. Ostrovskii, "Value distribution of meromorphic functions" , Moscow (1970) (In Russian) |
| [3] | V.P. Petrenko, "Growth of meromorphic functions of finite lower order" Math. USSR Izv. , 3 : 2 (1969) pp. 391–432 Izv. Akad. Nauk SSSR Ser. Mat. , 33 : 2 (1969) pp. 414–454 |
Comments
An 
-point of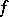 
is a point 
such that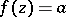 
.
Exceptional value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exceptional_value&oldid=32871