Herglotz formula
An integral relation between two closed isometric oriented regular surfaces. Let local coordinates  and
and  be introduced on the surfaces
be introduced on the surfaces 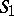 and
and 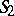 so that equality of the coordinates realizes an isometric mapping. Let
so that equality of the coordinates realizes an isometric mapping. Let
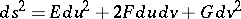 |
be the first fundamental form, having the same coefficients for both surfaces in the given coordinates, let 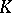 be the Gaussian curvature, let
be the Gaussian curvature, let 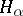 be the mean curvatures, and let
be the mean curvatures, and let
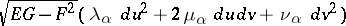 |
be the second fundamental forms of the surfaces 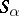 . Herglotz' formula then takes the following form:
. Herglotz' formula then takes the following form:
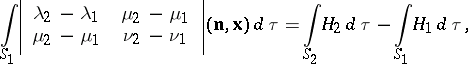 |
where 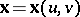 is the position vector of
is the position vector of 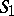 ,
,  is the unit vector of the normal to
is the unit vector of the normal to 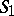 and
and 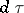 is the surface element. It was obtained by G. Herglotz [1].
is the surface element. It was obtained by G. Herglotz [1].
References
| [1] | G. Herglotz, "Ueber die Starrheit von Eiflächen" Abh. Math. Sem. Univ. Hamburg , 15 (1943) pp. 127–129 |
| [2] | N.V. Efimov, "Qualitative questions of the theory of deformations of surfaces" Uspekhi Mat. Nauk , 3 : 2 (1948) pp. 47–158 (In Russian) |
Comments
This formula can be used to prove rigidity or congruence theorems for surfaces. For related formulas and results see [a1].
References
| [a1] | H. Huck, R. Roitzsch, U. Simon, W. Vortisch, R. Walden, B. Wegner, W. Wendland, "Beweismethoden der Differentialgeometrie im Grossen" , Lect. notes in math. , 335 , Springer (1973) |
| [a2] | W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German) |
Herglotz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Herglotz_formula&oldid=32870