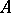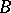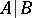Sheffer stroke

Sheffer bar

A logical operation, usually denoted by , given by the following truth table:'

<tbody> </tbody> T T F T F T F T T F F T

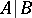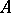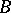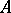Thus, the assertion means that and are incompatible, i.e. are not true simultaneously. All other logical operations can be expressed by the Sheffer stroke. For example, the assertion (the negation of ) is equivalent to the assertion 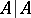; the disjunction 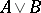of two assertions 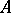and 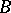is expressed as:

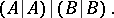The conjunction and the implication 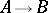are expressed as 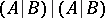and 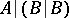, respectively. Sheffer's stroke was first considered by H. Sheffer.

References

[1]	H.M. Sheffer, "A set of five independent postulates for Boolean algebras, with applications to logical constants" Trans. Amer. Math. Soc. , 14 (1913) pp. 481–488

Comments

The Sheffer stroke operation is also called alternative denial.

References

[a1]	S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. 139
[a2]	W. Marek, J. Onyszkiewicz, "Elements of logic and the foundations of mathematics in problems" , Reidel & PWN (1982) pp. 4