Minimal propositional calculus
From Encyclopedia of Mathematics
minimal calculus of expressions
The logical calculus obtained from the positive propositional calculus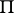 
by the addition of a new connective 
(negation) and the axiom scheme
 |
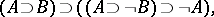which is called the law of reductio ad absurdum.
The minimal propositional calculus is distinguished by the fact that in it not every formula is deducible from "false" , that is, from a formula of the form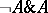 
. The minimal propositional calculus can be obtained from the calculus 
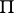in another way by adding to the language instead of the connective 
a new propositional constant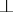 
(falsehood) without the addition of new axiom schemes. Here the formula 
serves as the negation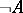 
of a formula 
.
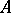References
| [1] | A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956) |
How to Cite This Entry:
Minimal propositional calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_propositional_calculus&oldid=32858
Minimal propositional calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_propositional_calculus&oldid=32858
This article was adapted from an original article by S.K. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article