Positive propositional calculus
A propositional calculus in the language 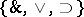 specified by the following 8 axiom schemes:
specified by the following 8 axiom schemes:
 |
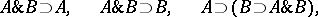 |
 |
and the modus ponens derivation rule. This calculus contains the part of the intuitionistic propositional calculus I (see Intuitionism) that is not dependent on negation: Any propositional formula not containing  (negation) is derivable in the positive propositional calculus if and only if it is derivable in I. One obtains the calculus I if one adds two axiom schemes to the positive propositional calculus:
(negation) is derivable in the positive propositional calculus if and only if it is derivable in I. One obtains the calculus I if one adds two axiom schemes to the positive propositional calculus:
1)  (antecedent negation law),
(antecedent negation law),
2) 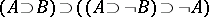 (reductio ad absurdum law).
(reductio ad absurdum law).
To derive I, instead of 2) one can take the weaker scheme:
2')  (law of partial reductio ad absurdum).
(law of partial reductio ad absurdum).
See also Implicative propositional calculus.
References
| [1] | A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956) |
| [2] | D. Hilbert, P. Bernays, "Grundlagen der Mathematik" , 1–2 , Springer (1968–1970) |
Positive propositional calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_propositional_calculus&oldid=32857