Truth-table reducibility
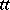-reducibility, diagram reducibility
A particular kind of algorithmic reducibility. Let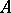 
and 
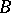be two sets of natural numbers. One says that 
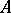is truth-table reducible to 
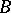(notation 
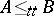) if there is an algorithm 
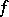that constructs for any natural number 
a Boolean function 
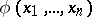(the function is given, for instance, by its table; the number of arguments of the function may depend on 
) and numbers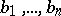 
such that 
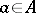is equivalent to the truth of 
.
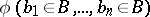The relation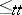 
is a pre-order on the set of all subsets of the natural numbers. To the relation 
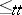corresponds an equivalence relation 
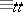, namely 
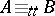if 
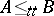and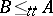 
. The equivalence classes for this relation are called truth-table degrees (or 
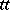-degrees); they form an upper semi-lattice.
In the theory of algorithms more special kinds of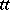 
-reducibility are also considered, for instance bounded 
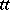-reducibility (
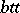-reducibility), defined by the additional requirement that the number of arguments of the function 
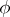does not depend on 
. If one simply takes the function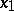 
for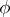 
, the reducibility is called many-one reducibility (notation: 
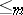). Intermediate reducibilities between 
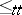and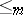 
, in particular all those mentioned above, are sometimes called reducibilities of truth-table type [2].
References
| [1] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
| [2] | A.N. Degtev, "Reducibilities of tabular type in the theory of algorithms" Russian Math. Surveys , 34 : 3 (1979) pp. 155–192 Uspekhi Mat. Nauk , 34 : 3 (1979) pp. 137–168 |
Comments
The various notions of reducibilities in recursion theory have found their resource-bounded analogues in the theory of computational complexity. In these theories the algorithm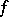 
is subjected to the further requirement that it can be computed in polynomial time or even logarithmic space.
References
| [a1] | R.E. Ladner, N.A. Lynch, A.L. Selman, "A comparison of polynomial time reducibilities" Theor. Comp. Sc. , 1 (1975) pp. 103–123 |
| [a2] | R.I. Soare, "Recursively enumerable sets and degrees, a study of computable functions and generated sets" , Springer (1987) |
Truth-table reducibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Truth-table_reducibility&oldid=32838