Orlicz class

The set 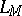of functions which satisfy the condition

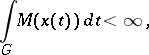where 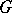is a bounded closed set in 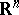, 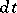is the Lebesgue measure, 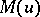is an even convex function (of a real variable) which is increasing for positive, and

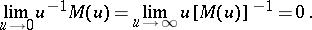These functions are called 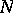-functions. The function 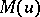can be represented as

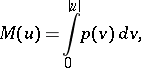where 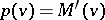does not decrease on ,

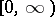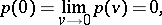and 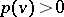when 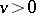. The function 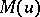and

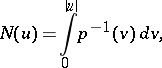where 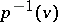is the inverse function of 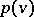, are called complementary functions. For example, if 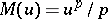, , 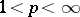then 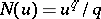, where 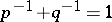. For a pair of complementary functions, the Young inequality

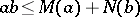holds.

The function 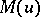is said to satisfy the 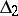-condition if there exist a 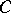and an 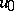such that 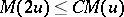for all 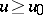. An Orlicz class is linear if and only if 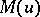satisfies the 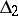-condition. The convexity of 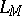follows from the Jensen inequality.

Let 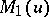and 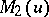be two 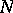-functions. In order that 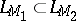it is necessary and sufficient that 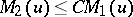for a certain 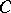and sufficiently large .

Orlicz classes were examined in [1] by W. Orlicz and Z. Birnbaum.

References

[1]	Z. Birnbaum, W. Orlicz, "Ueber die Verallgemeinerungen des Begriffes der zueinander konjugierten Potenzen" Studia Math. , 3 (1931) pp. 1–67
[2]	M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian)

References

[a1]	W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971)