Bendixson criterion

A theorem that permits one to establish the absence of closed trajectories of dynamical systems in the plane, defined by the equation

(*)

The criterion was first formulated by I. Bendixson [1] as follows: If in a simply-connected domain 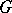the expression 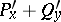has constant sign (i.e. the sign remains unchanged and the expression vanishes only at isolated points or on a curve), then the system (*) has no closed trajectories in the domain 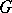. This criterion was generalized by H. Dulac [2] as follows: If 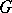is a simply-connected domain in the 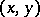-plane, if the functions 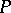and , and 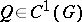if a function 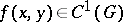can be found such that

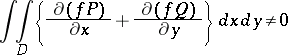for any simply-connected subdomain 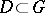, then the domain 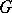does not contain any simple rectifiable closed curve consisting of trajectories and singular points of the system (*). If the domain 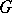is an annulus, a similar theorem states that a closed trajectory of (*), if it exists, is unique. A generalization applying to the case of system (*) with cylindrical phase space [3] is also possible.

References

[1]	I. Bendixson, "Sur les courbes définies par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88
[2]	H. Dulac, "Récherches des cycles limites" C.R. Acad. Sci. Paris Sér. I Math. , 204 (1937) pp. 1703–1706
[3]	A.A. Andronov, A.A. Vitt, A.E. Khaikin, "Theory of oscillators" , Pergamon (1966) (Translated from Russian)

Comments

Bendixson's criterion is also called the Poincaré–Bendixson theorem.

References

[a1]	A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian)