Discriminant curve

of an ordinary first-order differential equation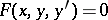

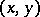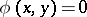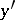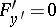The set of points of the plane whose coordinates satisfy the equation obtained by the elimination of from the relations and or by elimination of 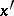from the relations 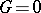and 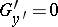, where 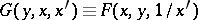(on the assumption that 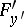in fact exists). If the discriminant curve for the equation is a non-empty set and does not degenerate into individual points, the curve (or each one of its branches) may:

1) be a solution of the equation 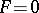at each point of which uniqueness is violated; the discriminant curve will then form the envelope of a family of integral curves (e.g. 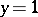and 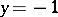for the equation 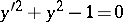(Fig. a); or 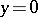for the equation (Fig. b));

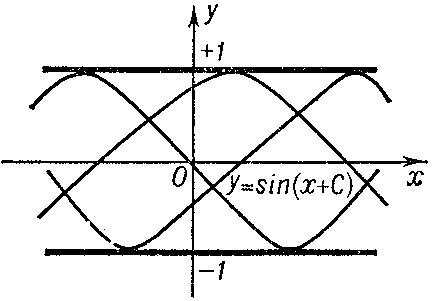
Figure: d033220a

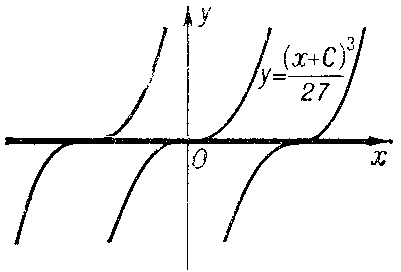
Figure: d033220b

2) be a solution of the equation at each point of which there is uniqueness (e.g. for the equation (Fig. c));

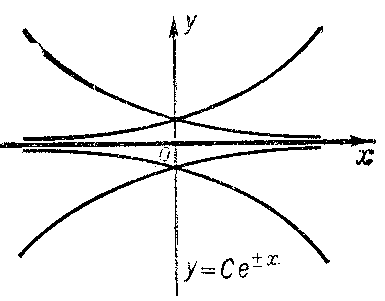
Figure: d033220c

3) not be a solution of the equation 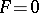. In this case the discriminant curve is either the set of cuspidal points of the integral curves (e.g. 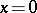for the equation 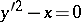(Fig. d)) or the set of osculation points of different integral curves (e.g. 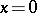for the equation 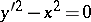(Fig. e)).

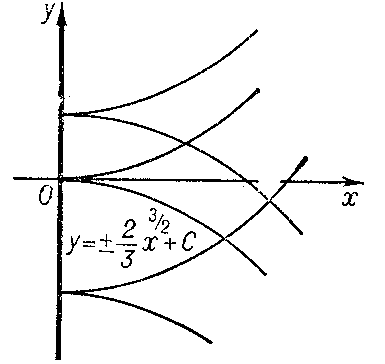
Figure: d033220d

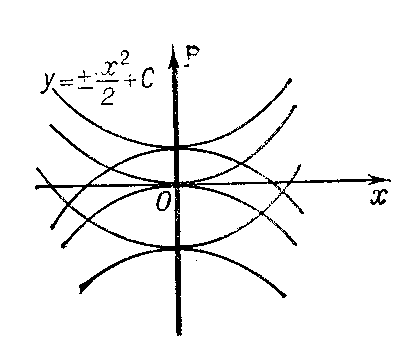
Figure: d033220e

The equation 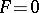, when 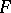is a polynomial in 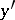, is also studied in the complex domain [2].

References

[1]	G. Sansone, "Equazioni differenziali nel campo reale" , 2 , Zanichelli (1949)
[2]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)