Enveloping series
for a number 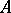
A series
 | (*) |
such that
 |
for all  . An enveloping series may converge or diverge; if it converges, then its sum is equal to
. An enveloping series may converge or diverge; if it converges, then its sum is equal to 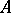 . The series (*) envelopes the real number
. The series (*) envelopes the real number 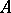 in the strict sense if the
in the strict sense if the  are real and if for all
are real and if for all 
 |
In this case  lies between any two successive partial sums of the series. For example, for
lies between any two successive partial sums of the series. For example, for  , the functions
, the functions 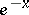 ,
,  ,
,  (
( ),
),  ,
,  ,
, 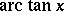 ,
, 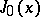 are enveloped in the strict sense by their MacLaurin series.
are enveloped in the strict sense by their MacLaurin series.
If, for 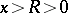 , the series
, the series
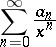 |
envelopes a function  taking real values, and if the numbers
taking real values, and if the numbers 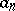 are real, then the signs of
are real, then the signs of 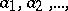 alternate and the series is enveloping in the strict sense. This series is an asymptotic expansion for
alternate and the series is enveloping in the strict sense. This series is an asymptotic expansion for 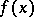 as
as  ; if it is divergent, then it is called a semi-convergent series. Such series are used for the approximate computation of
; if it is divergent, then it is called a semi-convergent series. Such series are used for the approximate computation of 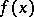 for large
for large  .
.
References
| [1] | G. Pólya, G. Szegö, "Problems and theorems in analysis" , Springer (1976) pp. Chapts. 1–2 (Translated from German) |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Comments
References
| [a1] | G.A. Scott, G.N. Watson, "Asymptotic formula occurring in electron theory" Quart. J. Math. , 47 (1917) pp. 312 |
Enveloping series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enveloping_series&oldid=32803