Nyquist criterion

A necessary and sufficient condition for the stability of a linear closed-loop system formulated in terms of properties of the open-loop system.

Consider the linear single input-linear single output system with the following transfer function:

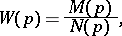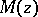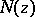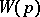where it is assumed that the degree of the polynomial does not exceed that of the polynomial (i.e. is a proper rational function). The original Nyquist criterion gives necessary and sufficient conditions for the stability of the closed-loop system with unity feedback 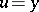. This is done in terms of the complex-valued function 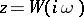of the real variable 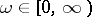(the amplitude-phase characteristic of the open-loop system) which describes a curve in the complex -plane, known as the Nyquist diagram. Suppose that the characteristic polynomial 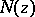of the open-loop system has 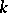, , 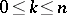roots with positive real part and 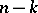roots with negative real part. The Nyquist criterion is as follows: The closed-loop system is stable if and only if the Nyquist diagram encircles the point 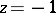in the counter-clockwise sense 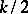times. (An equivalent formulation is: The vector drawn from 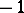to the point 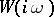describes an angle 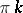in the positive sense as 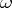goes from to .)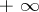

This criterion was first proposed by H. Nyquist [1] for feedback amplifiers; it is one of the frequency criteria for the stability of linear systems (similar, e.g., to the Mikhailov criterion, see [2], [3]). It is important to note that if the equations of some of the elements of the systems are unknown, the Nyquist diagram can be constructed experimentally, by feeding a harmonic signal of variable frequency to the input of the open feedback [4].

Generalizations of this criterion have since been developed for multivariable, infinite-dimensional and sampled-data systems, e.g. [5], , , .

References

[1]	H. Nyquist, "Regeneration theory" Bell System Techn. J. , 11 : 1 (1932) pp. 126–147
[2]	B.V. Bulgakov, "Oscillations" , Moscow (1954) (In Russian)
[3]	M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian)
[4]	Ya.N. Roitenberg, "Automatic control" , Moscow (1978) (In Russian)
[5]	L.S. Gnoenskii, G.A. Kamenskii, L.E. El'sgol'ts, "Mathematical foundations of the theory of control systems" , Moscow (1969) (In Russian)

Comments

For generalizations of the Nyquist criterion in various directions, see [a1].

References

[a1]	C.A. Desoer, M. Vidyasagar, "Feedback systems: input-output properties" , Acad. Press (1975)
[a2]	C.A. Desoer, "A general formulation of the Nyquist stability criterion" IEEE Trans. Circuit Theory , CT-12 (1965) pp. 230–234
[a3]	C.A. Desoer, Y.T. Wang, "On the generalized Nyquist stability criterion" IEEE Trans. Autom. Control , AC-25 (1980) pp. 187–196
[a4]	F.M. Callier, C.A. Desoer, "On simplifying a graphical stability criterion for linear distributed feedback systems" IEEE Trans. Automat. Contr. , AC-21 (1976) pp. 128–129
[a5]	J.M.E. Valenca, C.J. Harris, "Nyquist criterion for input-output stability of multivariable systems" Int. J. Control , 31 (1980) pp. 917–935
[a6]	P. Faurre, M. Depeyrot, "Elements of system theory" , North-Holland (1977)