Young symmetrizer
From Encyclopedia of Mathematics
An element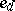 
of the group ring of the symmetric group 
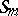defined by the Young tableau 
of order 
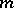by the following rule. Let 
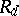(respectively, 
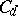) be the subgroup of 
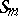consisting of all permutations permuting the numbers 
in each row (respectively, column) in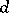 
. Further, put
 |
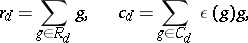where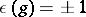 
is the parity of 
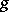. Then 
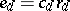(sometimes one defines 
).
The basic property of a Young symmetrizer is that it is proportional to a primitive idempotent of the group algebra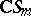 
. The coefficient of proportionality is equal to the product of the lengths of all hooks of 
.
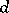Comments
The ideal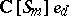 
is isomorphic to the Specht module of 
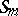defined by the Young tableau 
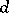. Cf. also Young tableau for references and more details.
How to Cite This Entry:
Young symmetrizer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_symmetrizer&oldid=32801
Young symmetrizer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_symmetrizer&oldid=32801
This article was adapted from an original article by E.B. Vinberg (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article