Empty-boxes test
A statistical test for verifying the hypothesis 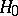 that an independent sample belongs to a given distribution. More explicitly, let
that an independent sample belongs to a given distribution. More explicitly, let 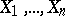 be an independent sample taken from a continuous distribution
be an independent sample taken from a continuous distribution 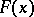 . The points
. The points  are chosen so that
are chosen so that 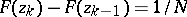 ,
,  . The test is constructed on the basis of the statistic
. The test is constructed on the basis of the statistic 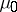 equal to the number of half-intervals
equal to the number of half-intervals 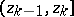 in which there is not a single observation
in which there is not a single observation 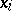 . This test has the following form: If
. This test has the following form: If  , then the hypothesis
, then the hypothesis 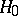 is accepted; if
is accepted; if 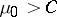 , then
, then 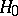 is rejected. The constant
is rejected. The constant 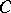 is chosen from the condition that the error of the first kind, that is, the probability that
is chosen from the condition that the error of the first kind, that is, the probability that 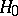 is rejected while it is true, is equal to a given value. One may calculate the constant
is rejected while it is true, is equal to a given value. One may calculate the constant 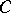 and estimate the power of the empty-boxes test for large
and estimate the power of the empty-boxes test for large  and
and 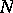 by using limit theorems for random distributions.
by using limit theorems for random distributions.
References
| [1] | V.F. [V.F. Kolchin] Kolčin, B.A. [B.A. Sevast'yanov] Sevast'janov, V.P. [V.P. Chistyakov] Čistyakov, "Random allocations" , Winston (1978) (Translated from Russian) |
Empty-boxes test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Empty-boxes_test&oldid=32789