Dirichlet formula
From Encyclopedia of Mathematics
for the number of divisors
The asymptotic formula
 |
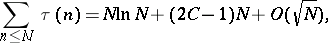where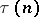 
is the number of divisors of 
and 
is the Euler constant. Obtained by P. Dirichlet in 1849; he noted that this sum is equal to the number of points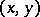 
with positive integer coordinates in the domain bounded by the hyperbola 
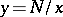and the coordinate axes, i.e. equal to
 |
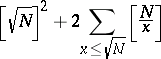where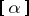 
denotes the integer part of 
.
References
| [1] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
Comments
See also Divisor problems.
How to Cite This Entry:
Dirichlet formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_formula&oldid=32774
Dirichlet formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_formula&oldid=32774
This article was adapted from an original article by A.F. Lavrik (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article