Moufang loop
A loop in which the following (equivalent) identities hold:
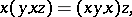 |
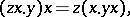 |
 |
These loops were introduced and studied by R. Moufang [1]. In particular, she proved the following theorem, showing that the loops of this class are close to groups: If the elements  ,
,  and
and  of a Moufang loop satisfy the associativity relation
of a Moufang loop satisfy the associativity relation  , then they generate an associative subloop, that is, a group (Moufang's theorem). A corollary of this theorem is the di-associativity of a Moufang loop: Any two elements of the loop generate an associative subloop.
, then they generate an associative subloop, that is, a group (Moufang's theorem). A corollary of this theorem is the di-associativity of a Moufang loop: Any two elements of the loop generate an associative subloop.
For commutative Moufang loops, which are defined by the single identity
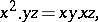 |
the following theorem holds: Every commutative Moufang loop with  generators is centrally nilpotent with nilpotency class not exceeding
generators is centrally nilpotent with nilpotency class not exceeding  (see [2]). Central nilpotency is defined analogously to nilpotency in groups (cf. Nilpotent group).
(see [2]). Central nilpotency is defined analogously to nilpotency in groups (cf. Nilpotent group).
If a loop is isotopic (cf. Isogeny) to a Moufang loop, then it is itself a Moufang loop, that is, the property of being a Moufang loop is universal. Moreover, isotopic commutative Moufang loops are isomorphic.
References
| [1] | R. Moufang, "Zur Struktur von Alternativkörpern" Math. Ann. , 110 (1935) pp. 416–430 |
| [2] | R.H. Bruck, "A survey of binary systems" , Springer (1958) |
Moufang loop. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moufang_loop&oldid=32766