Domain of individuals (in logic)
From Encyclopedia of Mathematics
universe
A term in model theory denoting the domain of variation of individual (object) variables of a given formal language of first-order predicate calculus. Each such language is completely described by the set
 |
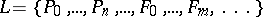where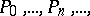 
are predicate symbols and 
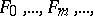are function symbols for each of which a number of argument places is given. A model 
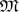(or an algebraic system) of 
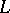is given by a non-empty set 
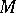and an interpreting function 
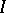, defined on 
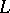and assigning an 
-place predicate to an 
-place predicate symbol, i.e. a subset of the Cartesian power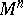 
of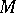 
, and an 
-place function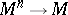 
to an 
-place function symbol. The set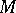 
is called the domain of individuals (or universe) of the model 
.
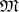References
| [1] | S.C. Kleene, "Mathematical logic" , Wiley (1967) |
| [2] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973) |
| [3] | Yu.L. Ershov, E.A. Palyutin, "Mathematical logic" , Moscow (1987) (In Russian) |
How to Cite This Entry:
Domain of individuals (in logic). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domain_of_individuals_(in_logic)&oldid=32761
Domain of individuals (in logic). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domain_of_individuals_(in_logic)&oldid=32761
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article