Asymptotically-efficient estimator

A concept which extends the idea of an efficient estimator to the case of large samples (cf. Efficient estimator). An asymptotically-efficient estimator has not been uniquely defined. Thus, in its classical variant it concerns the asymptotic efficiency of an estimator in a suitably restricted class 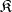of estimators. In fact, let 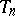be a consistent estimator of a one-dimensional parameter 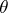constructed from a random sample of size . 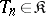Then if the variance 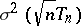exists, and if it is bounded from below, as 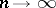, by the inverse of the Fisher amount of information corresponding to one observation. An estimator 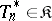which attains the lower bound just mentioned is asymptotically efficient. Under certain conditions this property is satisfied by the maximum-likelihood estimator for 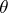, which makes the classical definition meaningful. If the asymptotically-efficient estimator 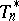exists, the magnitude

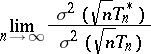is called the asymptotic relative efficiency of 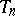. Certain variants of the concept of an asymptotically-efficient estimator are due to R.A. Fisher, C.R. Rao and others.

References

[1]	C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965)

Comments

More modern definitions of this concept are due to J. Hajek, L. LeCam and others.

References

[a1]	J.A. Ibragimov, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian)