Deviation of an approximating function
From Encyclopedia of Mathematics
The distance 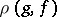 between the approximating function
between the approximating function 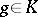 and a given function
and a given function 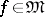 . In one and the same class
. In one and the same class 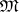 different metrics
different metrics 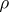 may be considered, e.g. the uniform metric
may be considered, e.g. the uniform metric
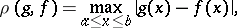 |
an integral metric
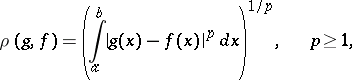 |
and other metrics. As the class 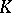 of approximating functions one may consider algebraic polynomials, trigonometric polynomials and also partial sums of orthogonal expansions of
of approximating functions one may consider algebraic polynomials, trigonometric polynomials and also partial sums of orthogonal expansions of 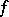 in an orthogonal system, linear averages of these partial sums as well as a number of other sets.
in an orthogonal system, linear averages of these partial sums as well as a number of other sets.
References
| [1] | P.L. Chebyshev, "Complete collected works" , 2 , Moscow-Leningrad (1947) (In Russian) |
| [2] | I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian) |
| [3] | V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian) |
| [4] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [5] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
Comments
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) |
| [a2] | A. Schönhage, "Approximationstheorie" , de Gruyter (1971) |
How to Cite This Entry:
Deviation of an approximating function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deviation_of_an_approximating_function&oldid=32753
Deviation of an approximating function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deviation_of_an_approximating_function&oldid=32753
This article was adapted from an original article by A.V. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article