Laguerre formula
A formula for calculating the angle between straight lines in Euclidean and pseudo-Euclidean spaces. Let 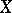 and
and 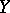 be the points at infinity on two straight lines
be the points at infinity on two straight lines  and
and 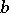 and let
and let 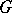 and
and 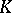 be the points of intersection of these lines with the absolute of the space. Then the angle
be the points of intersection of these lines with the absolute of the space. Then the angle 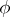 between these lines can be expressed in terms of the cross ratio
between these lines can be expressed in terms of the cross ratio 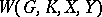 :
:
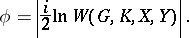 |
For two-dimensional pseudo-Euclidean space,  and
and  are the direction vectors of the isotropic lines passing through the point of intersection of the lines
are the direction vectors of the isotropic lines passing through the point of intersection of the lines  and
and 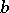 .
.
The formula was introduced by E. Laguerre .
A formula according to which, for all curves on a given surface that touch at some point, the quantity
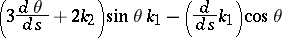 |
is invariant, where 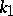 and
and 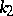 are the curvature and the torsion of the curve,
are the curvature and the torsion of the curve,  is the angle between the principal normal of the curve and the normal to the surface, and
is the angle between the principal normal of the curve and the normal to the surface, and  is the natural parameter on the curve. The formula was obtained by E. Laguerre (1870, see [2]).
is the natural parameter on the curve. The formula was obtained by E. Laguerre (1870, see [2]).
References
| [1] | E. Laguerre, "Sur la théorie des foyers" Nouv. Ann. Math. , 12 (1853) pp. 57–66 |
| [2] | E. Laguerre, "Oeuvres" , 2 , Chelsea, reprint (1972) |
| [3] | B.A. Rozenfel'd, "Non-Euclidean geometry" , Moscow (1955) (In Russian) |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
Laguerre formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laguerre_formula&oldid=32750