Phase equilibrium diagram

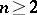The projection onto the plane of two arbitrary thermodynamical variables of those regions of the surface of the equilibrium states in the space of the complete family of thermodynamical variables that correspond to -phase states, , of the thermodynamical system. In the case of a one-component system the regions of this surface are cylindrical surfaces and they project onto the 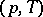-plane (pressure-temperature plane) in the form of a curve, the general form of its equation — equality of the chemical potentials of different phases, — can in the case of phase transition of the first kind be written in the form of the Clapeyron–Clausius equation

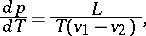where is the latent heat of the transition, and and are the specific volumes for the first and the second phases. A three-phase state is represented by a point, called a triple point.

References

[1]	R. Kubo, "Thermodynamics" , North-Holland (1968)

References

[a1]	L.D. Landau, E.M. Lifshitz, "Statistical physics" , 1 , Pergamon (1980) (Translated from Russian)
[a2]	E. Fermi, "Thermodynamics" , Dover, reprint (1956)