Independent measurable decompositions

independent measurable partitions, of a space with a normalized measure

Two measurable partitions and such that if 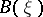and are Boolean -algebras of measurable sets consisting entirely of elements of 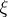and , respectively, then the elements of one of them are independent of the elements of the other in the sense of probability theory: 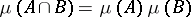for 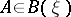, 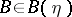. Under these conditions, if a measurable partition that is a refinement of both 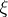and 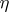coincides 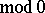with the partition into single points, then 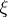and are said to be independent complements of one another. Conditions are known for a measurable partition of a Lebesgue space to have an independent complement.

References

[1]	V.A. Rokhlin, "On the main notions of measure theory" Mat. Sb. , 25 : 1 (1949) pp. 107–150 (In Russian)
[2]	M.P. Ershov, "Rokhlin's theorem on independent complementation" Uspekhi Mat. Nauk , 32 : 1 (1977) pp. 187–188 (In Russian)

Comments

See also Measurable decomposition.

References

[a1]	I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian)
[a2]	W. Parry, "Topics in ergodic theory" , Cambridge Univ. Press (1981)