Oscillator, harmonic
A system with one degree of freedom whose oscillations are described by the equation
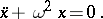 |
The phase trajectories are circles, the period of the oscillations,  , does not depend on the amplitude. The potential energy of a harmonic oscillator depends quadratically on
, does not depend on the amplitude. The potential energy of a harmonic oscillator depends quadratically on  :
:
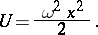 |
Examples of harmonic oscillators are: small oscillations of a pendulum, oscillations of a material point fastened on a spring with constant rigidity, and the simplest electric oscillatory circuit. The terms "harmonic oscillator" and "linear oscillatorlinear oscillator" are often used as synonyms.
The oscillations of a quantum-mechanical linear oscillator are described by the Schrödinger equation
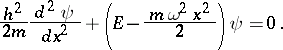 |
Here,  is the mass of a particle,
is the mass of a particle, 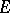 is its energy,
is its energy,  is the Planck constant, and
is the Planck constant, and 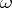 is the frequency. A quantum-mechanical linear oscillator has a discrete spectrum of energy levels,
is the frequency. A quantum-mechanical linear oscillator has a discrete spectrum of energy levels, 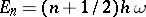 ,
,  ; the corresponding eigen functions can be expressed in terms of Hermite functions (cf. Hermite function).
; the corresponding eigen functions can be expressed in terms of Hermite functions (cf. Hermite function).
The term "oscillator" is used in relation to (mechanical or physical) systems with a finite number of degrees of freedom whose motion is oscillatory (e.g. a van der Pol oscillator — a multi-dimensional linear oscillator representing the oscillations of a material point situated in a potential force field with a potential which is a positive-definite quadratic form in the coordinates, see van der Pol equation). There is evidently no unique interpretation of the term "oscillator" , or even of "linear oscillator" .
References
| [1] | L.I. Mandel'shtam, "Lectures on the theory of oscillations" , Moscow (1972) (In Russian) |
| [2] | L.D. Landau, E.M. Lifshitz, "Quantum mechanics" , Pergamon (1965) (Translated from Russian) |
Comments
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a2] | L.I. Schiff, "Quantum mechanics" , McGraw-Hill (1949) |
Oscillator, harmonic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillator,_harmonic&oldid=32692