Brunn-Minkowski theorem
Let 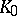 and
and  be convex sets in an
be convex sets in an  -dimensional Euclidean space; let
-dimensional Euclidean space; let 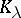 ,
, 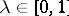 , be the set of points which divide segments with end points at any points of the sets
, be the set of points which divide segments with end points at any points of the sets 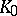 and
and 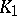 in the ratio
in the ratio 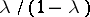 (a linear combination of
(a linear combination of 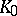 and
and 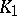 ); and let
); and let  be the
be the  -th power root of the volume of the set
-th power root of the volume of the set 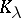 . Then
. Then 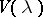 is a concave function of
is a concave function of  , i.e. the inequality
, i.e. the inequality
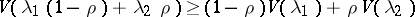 |
is valid for all  . The function
. The function 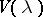 is linear (and the inequality then becomes an equality) if and only if
is linear (and the inequality then becomes an equality) if and only if 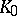 and
and 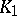 are homothetic. The Brunn–Minkowski theorem can be generalized to linear combinations of several convex sets. It is used to solve extremal and uniqueness problems. It was discovered by H. Brunn in 1887, and completed and rendered more precise in 1897 by H. Minkowski.
are homothetic. The Brunn–Minkowski theorem can be generalized to linear combinations of several convex sets. It is used to solve extremal and uniqueness problems. It was discovered by H. Brunn in 1887, and completed and rendered more precise in 1897 by H. Minkowski.
References
| [1] | H. Busemann, "Convex surfaces" , Interscience (1958) |
| [2] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) |
Comments
References
| [a1] | K. Leichtweiss, "Konvexe Mengen" , Springer (1979) |
Brunn-Minkowski theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brunn-Minkowski_theorem&oldid=32691