Hardy theorem
From Encyclopedia of Mathematics
in the theory of functions of a complex variable
If 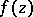 is a regular analytic function in the disc
is a regular analytic function in the disc 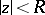 ,
, 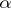 is a positive number, and if
is a positive number, and if
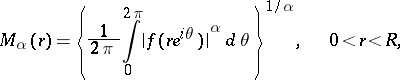 |
is the average value, then 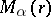 is a non-decreasing function of
is a non-decreasing function of  that is logarithmically convex relative to
that is logarithmically convex relative to 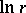 (cf. Convexity, logarithmic). The theorem was established by G.H. Hardy [1].
(cf. Convexity, logarithmic). The theorem was established by G.H. Hardy [1].
The assertion on the logarithmic convexity remains valid for a function  that is regular in an annulus
that is regular in an annulus 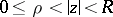 (see [1]).
(see [1]).
Hardy's theorem generalizes to subharmonic functions (cf. Subharmonic function) in a ball of 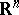 ,
, 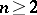 (see also [2]).
(see also [2]).
References
| [1] | G.H. Hardy, "The mean value of the modulus of an analytic function" Proc. London. Math. Soc. (2) , 14 (1915) pp. 269–277 |
| [2] | I.I. Privalov, "Subharmonic functions" , Moscow-Leningrad (1937) (In Russian) |
Comments
References
| [a1] | T. Radó, "Subharmonic functions" , Springer (1937) |
| [a2] | P.L. Duren, "Theory of 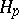 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
| [a3] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 |
How to Cite This Entry:
Hardy theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_theorem&oldid=32687
Hardy theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_theorem&oldid=32687
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article