Specht property

A variety of some universal algebras (e.g. groups, semi-groups, associative, Lie, Jordan, etc., rings and algebras; cf. also Variety of universal algebras; Universal algebra) is the class of all algebras satisfying a given system of identical relations (polynomial identities in the case of rings and algebras over a field). The description of the identities of concrete varieties and algebras is one of the central problems in the theory. A variety is finitely based (or has a finite basis for its identities) if it can be defined by a finite number of identities. A variety satisfies the Specht property if it itself and all its subvarieties are finitely based. The problem of existence of infinitely based varieties of groups was raised by B.H. Neumann in his thesis in 1935, see also [a11], and for associative algebras by W. Specht [a16] in 1950. Nowadays (2001), the finite basis problem for all main classes of universal algebras is known also as the Specht problem. The investigations are in two directions: to show that classes of varieties satisfy the Specht property and to construct counterexamples. For comments and results for groups, semi-groups and algebras see [a1], [a6], [a7], [a12] and [a2], [a8].

The positive results include the Specht property for varieties generated by finite objects with reasonable good structure (e.g. groups, associative, Lie, Jordan rings and algebras over finite fields), classes of groups, rings and algebras satisfying some specific identities (e.g. nilpotent or metabelian groups and Lie algebras). One of the most important results in this direction is the positive solution by A.R. Kemer of the Specht problem for associative algebras over a field of characteristic zero, see [a7].

It is relatively easy to construct counterexamples to the Specht problem for sufficiently general algebras. There exist also finite semi-groups [a14] and finite non-associative rings [a15] without finite bases for their identities. The first counterexample to the finite basis problem for groups was given by A.Yu. Ol'shanskii [a13] in 1970. The simplest example is due to Yu.G. Kleiman [a9], [a10] and R.M. Bryant [a4], who showed that the system of group identities 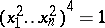, , 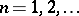does not follow from any of its finite subsystems. The first example of a Lie algebra without a finite basis for its identities was given by M.R. Vaughan-Lee [a17] in characteristic two, and then generalized to any field of positive characteristic by V. Drensky [a5] and Kleiman (unpublished). The variety of Vaughan-Lee is defined by the centre-by-metabelian identity 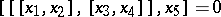and the identities 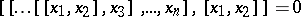, 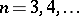. He also showed that over an infinite field of characteristic two the Lie algebra of all 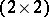-matrices has no finite basis of its polynomial identities. Recently (1999), A.Ya. Belov [a3], see also [a18], constructed an example of a non-finitely based variety of associative algebras over any field of positive characteristic.

Presently (2001), the Specht problem is still open for Lie algebras over a field of characteristic zero. Many questions concerning finite bases of polynomial identities are naturally connected also with other problems at the meeting point of algebra and logic, in particular with various algorithmic problems, see [a8].

References

[a1]	Yu.A. Bahturin, "Identical relations in Lie algebras" , VNU Press (1987) (In Russian)
[a2]	Yu.A. Bahturin, A.Yu. Olshanskii, "Identities" A.I. Kostrikin (ed.) I.R. Shafarevich (ed.) , Algebra II , Encyclopedia Math. Sci. , 18 , Springer (1991) pp. 107–221
[a3]	A.Ya. Belov, "On nonspechtian varieties" Fundam. i Prikladn. Mat. , 5 : 1 (1999) pp. 47–66 (In Russian)
[a4]	R.M. Bryant, "Some infinitely based varieties of groups" J. Austral. Math. Soc. , 16 (1973) pp. 29–32
[a5]	V. Drensky, "Identities in Lie algebras" Algebra and Logic , 13 (1974) pp. 150–165 Algebra i Logika , 13 (1974) pp. 265–290
[a6]	V. Drensky, "Free algebras and PI-algebras" , Springer (1999)
[a7]	A.R. Kemer, "Ideals of identities of associative algebras" , Transl. Math. Monographs , 87 , Amer. Math. Soc. (1991)
[a8]	O.G. Kharlampovich, M.V. Sapir, "Algorithmic problems in varieties" Internat. J. Algebra Comput. , 5 (1995) pp. 379–602
[a9]	Yu.G. Kleiman, "The basis of a product variety of groups I" Math. USSR Izv. , 7 (1973) pp. 91–94 Izv. Akad. Nauk. SSSR Ser. Mat. , 37 (1973) pp. 95–97
[a10]	Yu.G. Kleiman, "The basis of a product variety of groups II" Math. USSR Izv. , 8 (1974) pp. 481–489 Izv. Akad. Nauk. SSSR Ser. Mat. , 38 (1974) pp. 475–483
[a11]	B.H. Neumann, "Identical relations in groups I" Math. Ann. , 114 (1937) pp. 506–525
[a12]	H. Neumann, "Varieties of groups" , Springer (1967)
[a13]	A.Yu. Olshanskii, "On the problem of a finite basis of identities in groups" Math. USSR Izv. , 4 (1970) pp. 381–389 Izv. Akad. Nauk. SSSR Ser. Mat. , 34 (1970) pp. 376–384
[a14]	P. Perkins, "Decision problems for equational theories of semigroups and general algebras" PhD Thesis Univ. California at Berkeley (1966)
[a15]	S.V. Polin, "Identities of finite algebras" Sib. Math. J. , 17 (1976) pp. 992–999 Sibirsk. Mat. Zh. , 17 (1976) pp. 1356–1366
[a16]	W. Specht, "Gesetze in Ringen I" Math. Z. , 52 (1950) pp. 557–589
[a17]	M.R. Vaughan-Lee, "Varieties of Lie algebras" Quart. J. Math. Oxford Ser. 2 , 21 (1970) pp. 297–308
[a18]	A.Ya. Belov, "Counterexamples to the Specht problem" Sb. Math. , 191 (2000) pp. 329–340 Mat. Sb. , 191 (2000) pp. 13–24