Measure of irrationality
From Encyclopedia of Mathematics
of a real number 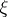
The function
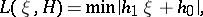 |
where the minimum is over all pairs 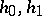 of integral rational numbers such that
of integral rational numbers such that
 |
The concept of the measure of irrationality is a particular case of those of the measure of linear independence and the measure of transcendency (cf. Linear independence, measure of; Transcendency, measure of). The measure of irrationality indicates how "well" the number 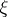 can be approximated by rational numbers. For all real irrational numbers one has
can be approximated by rational numbers. For all real irrational numbers one has
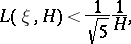 |
but for any 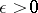 and almost-all (in the sense of the Lebesgue measure) real numbers
and almost-all (in the sense of the Lebesgue measure) real numbers 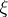 ,
,
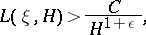 |
where 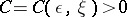 . However, for any function
. However, for any function 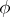 with
with 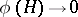 as
as 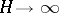 and
and 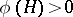 , there exists a number
, there exists a number 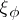 such that for all
such that for all 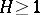 ,
,
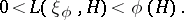 |
References
| [1] | A.Ya. Khinchin, "Continued fractions" , Univ. Chicago Press (1964) (Translated from Russian) |
How to Cite This Entry:
Measure of irrationality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measure_of_irrationality&oldid=32680
Measure of irrationality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measure_of_irrationality&oldid=32680
This article was adapted from an original article by A.I. Galochkin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article